Lower plants like ferns and horsetails have as growth points
apical cells that have the shape of an inverted pyramid or parabolic dish.
In higher plants growth does not arise from a single cell, but from growth zones, called
meristems, in which groups of dividing cells occur. (Meristems consist of undifferentiated cells that have the capacity to divide; meristos means 'divided' in Greek). The first meristems can be found even before seed germination: during the early development of the plant embryo, two
apical meristems arise, at the tip of the rootlet and at the tip of the shootlet. These two apical meristems lead to the formation of the primary meristems from which primary tissues arise: root tissue develops from the apical root meristem and leaves and original tissue layers in the stem develop from the
apical shoot meristem.
Voorbeelden: topmeristemen in embryo's en groeiende planten
| Apical meristem in a young plant embryo and a plantlet |
 |
 |
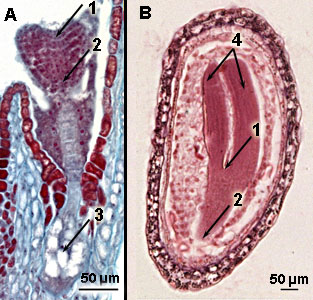
Top or apical meristems in embryo's of the Shepherd's purse
A. Young 'heart-shaped' embryo and B older 'torpedo-shaped' embryo
1 = top or apical shoot meristem; 2 = top or apical root meristem; 3 = suspensor; 4 = cotyledons | Meristem of Coleus
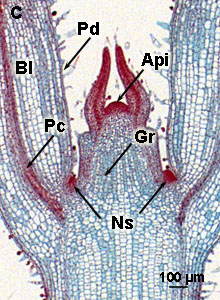
Api = apical meristem; Gr = ground meristem; Pd = protoderm; Pc = procambium; Ns = New side shoot; Bl = Blade
To a photograph of the apical meristem in Coleus taken with an electron microscope |
The primary meristems, which arise from the apical shoot meristem, lead to the formation of the following primary tissues in the stem:
- The protoderm (Pd) from which the epidermis arises
- The ground meristem (Gr) that forms ground tissue
- The procambium (Pc) from which vascular bundles develop in which differentiation between xylem (for transport of water from root to leaves) and phloem (for transport of sugars) occurs.
In dicots at a more mature stage, cambium that will form secondary vascular tissues is generated from the procambium (more here about in the pages on secondary meristems
New side shoots (Ns) are formed by mitotic divisions in the cortex, just below the epidermis, parallel to the surface (periclinal). In a later stage also perpendicularly-oriented divisions (anticlinal) occur and finally also in the epidermis (exclusively anticlinal).
The apical meristem remains active during the whole development of the plant, in both monocots and dicots; in the primary meristematic zones increase in length through cell division (mitosis) occurs. Besides division, cell stretching and expansion contribute to the increase in size of the plant.
| Organization of the apical shoot meristem |
| Cellular layers and division planes |
Elodea (1,2,3)
(Monocot) |
Coleus (4,5)
(Dicot) |
Organization of the apical shoot meristem in Elodea (monocot; left column) and in Coleus (dicot; right column).
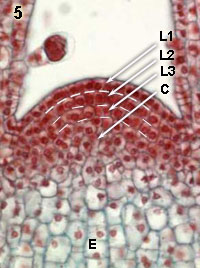
These apical meristems are made of small, rapidly dividing cells. In the most superficial layer of the apical shoot meristem, called tunica, the divisions are nearly exclusively anticlinal (see explantion hereabove). By contrast, in the group of cells below the tunica, called corpus, anticlinal, periclinal aas well as oblique divisions occur, such that the volume of the stem increases. The organization of tunica and corpus differs among species. In Elodea, for example, the tunica consists of a single layer, whereas in Coleus a two-cell layer is observed (indicated by L1 and L2). L3 indicates the so-called initial layer of the corpus (C) in this species. After division newly formed cells expand (E), what contributes to the growth.
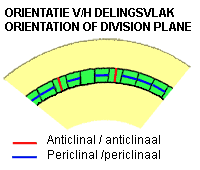
Anticlinal divisions: the newly formed cell wall is perpendicular to the surface of the tissue
Periclinal divisions: the newly formed cell wall is parallel to the surface of the tissue
| 
|

|

|
|
Growth and stem structure in monocots, dicots and in woody Gymnosperms

Along with the increase in foliage and branching of a growing stem, the need for new vascular, filling and supportive tissues also raises. In dicots (Example: Coleus and sunflower) but also in woody gymnosperms (here left, see also examples of microscopic slides of the stem of
pine) a new division layer (cambium layer) arises which is involved in lateral expansion, so-called
secondary growth (more about thickening growth in the stem in the pages on
secondary meristems).
On the other side in monocots (Examples: Elodea and maize)
primary growth is the
only way to add new cells to the plant body, namely by divisions in the apical meristem, protoderm, procambium and groundmeristem. Palmbomen, which also belong to the monocots, know a kind of pseudo-thickening growth: however, this mode of lateral expansion of the stem still relies on division of cells derived from the -primary- apical meristem. Among monocotyledonous plants, only a very small group to which
Dracaena belongs, shows true secondary growth.
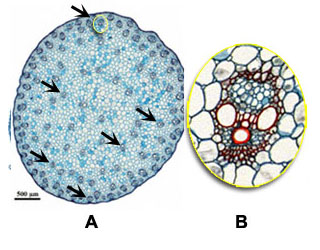
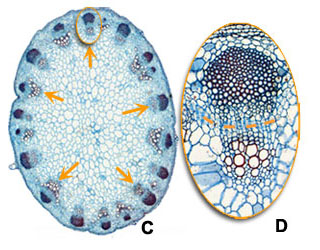
Another characteristics of monocots, besides the absence of vascular cambium, is that the vascular bundles are scattered through the ground tissue of the stem (black arrows in overview A on maize), and that each vascular bundle forms a close structure (presence of a sheath, see B). In dicots the vascular bundles are arranged in an open ring in the young stem (orange arrows in overview C in sunflower) and within vascular bundles xylem and phloem are divided by a cambium layer (dashed line in D) from which further growth and differentiation can follow.
| Structure of the stem: monocots versus dicots |
Monocot, e.g. Maize (A and B) | Dicot, e.g. Sunflower (C and D) |
| In monocots vascular bundles are scattered inside the stem (black arrows in A). Each vascular bundle is surrounded by a sheath. There is no cambium layer involved in secondary growth (B) |
In dicots vascular bundles are arranged as islands in a ring (orange arrows in C). A cambium layer is present (dashed line in D) from which thickening growth will rise. |
 |  |
 |
 | Maize plants and palmtrees are both monotocots. In contrast to dicots like the sunflower here richt, they do now show secondary thickening growth. The increase in perimeter of the trunk in palmtrees originates from a broad apical meristem. |

|